| BLOG |
Carl McTague
mathematician, composer, photographer, fiddler |
How to Recognize Generators for String Bordism
A key result of my paper:
The Cayley Plane and String Bordism, Geometry & Topology 18-4 (2014), 2045–2078.
unmentioned in the abstract or introduction—and likely of independent interest—is the following characteristic-number-theoretic criterion for a set to generate the String bordism ring (with 6 inverted).
Theorem 4. A set $S$ generates the ring $\pi_*\mathrm{MO}\langle8\rangle[1/6]$ if:
- For each integer $n>1$, there is an element $M^{4n}$ of $S$ such that for any prime $p>3$: $$\begin{align*} \mathrm{ord}_p \big( \mathrm{s}_n[M^{4n}] \big) = \begin{cases} 1 & \text{if $2n=p^i-1$ or $2n=p^i+p^j$ for some integers $0 \le i \le j$} \\ 0 & \text{otherwise} \end{cases} \end{align*}$$ where $\mathrm{s}_n[M]$ is the characteristic number corresponding to the $n$th power sum symmetric polynomial $\sum x_i^n$ in the Pontrjagin roots of the tangent bundle of $M$, and $\mathrm{ord}_p(-)$ its $p$-adic order, i.e. the heighest power of $p$ which divides it.
- For each prime $p>3$ and each pair of integers $0<i<j$, there is an element $N^{2(p^i+p^j)}$ of $S$ such that: $$\begin{align*} \mathrm{s}_{(p^i+p^j)/2}[N^{2(p^i+p^j)}]&=0 \\ \mathrm{s}_{(p^i+1)/2,(p^j-1)/2}[N^{2(p^i+p^j)}] &\not\equiv 0 \mod p^2 \end{align*}$$ where $\mathrm{s}_{m,n}[N]$ is the characteristic number corresponding to the symmetric polynomial $\sum_{i\ne j} x_i^mx_j^n$ in the Pontrjagin roots of the tangent bundle of $N$.
This is a consequence of Hovey’s calculation of:
The homotopy of $\mathrm{MString}$ and $\mathrm{MU}\langle6\rangle$ at large primes, Algebr. Geom. Topol. 8 (2008), 2401–2414.
which itself builds on Hopf-ring-theoretic work of Ravenel and Wilson. It should be compared with the analogous result for the oriented bordism ring (with 2 inverted):
Theorem (Novikov, cf. Stong p. 180). A sequence $\{M^{4n}\}_{n\ge1}$ generates the ring $\pi_*\mathrm{MSO}[1/2]$ if and only if:
- For any integer $n>0$ and any odd prime $p$: $$\begin{align*} \mathrm{ord}_p \big( \mathrm{s}_n[M^{4n}] \big) = \begin{cases} 1 & \text{if $2n=p^i-1$ for some integer $i>0$} \\ 0 & \text{otherwise} \end{cases} \end{align*}$$
References
-
Robert Stong, Notes on Cobordism Theory, Princeton University Press, 1968.
-
John Milnor, Characteristic Classes, Princeton University Press, 1974.
Binomial Coefficients and Villainy
Sherlock Holmes’s criminal archenemy Professor Moriarty was modeled on Hopkins mathematics professor Simon Newcomb (1835–1909).
“At the age of twenty-one [Moriarty] wrote a treatise upon the binomial theorem, which has had a European vogue,” and was “the celebrated author of The Dynamics of an Asteroid, a book which ascends to such rarefied heights of pure mathematics that it is said that there was no man in the scientific press capable of criticizing it” [from “The Final Problem” (1893) and The Valley of Fear (1914) by Arthur Conan Doyle].
At the age of nineteen Newcomb wrote an unpublished New Demonstration of the Binomial Theorem and was a celebrated expert on the dynamics of the solar system. He was also notoriously malicious. For example, he destroyed Charles Sanders Peirce’s career by secretly changing Hopkins president Daniel Coit Gilman’s mind about granting Peirce tenure, this after having been the favorite PhD student of Peirce’s father Benjamin Peirce at Harvard. (Newcomb was incidentally the maternal grandfather of Hassler Whitney.)
These and further similarities between Moriarty and Newcomb were first noted by Ronald Schorn in 1978, and the case for direct inspiration was convincingly made by Bradley Schaefer in 1993 (by arguing that Doyle would have known of Newcomb through close friend Alfred Drayson):
Sherlock Holmes and some astronomical connections, Journal of the British Astronomical Association, Vol. 103, No. 1 (1993), pp. 30–34.
The possibility of completing the square:
| Holmes | — | Moriarty |
| ⋮ | | | |
| CS Peirce | — | Newcomb |
is suggested by the existence of the book:
Umberto Eco & Thomas A. Sebeok (eds.), The Sign of Three: Dupin, Holmes, Peirce, Indiana University Press (1984).
References
-
Joseph Brent, Charles Sanders Peirce, A Life, Indiana University Press, Bloomington, 1998.
-
Prof Stephen Hawking: make me a Bond villain, The Telegraph, London, 1 Dec 2014. [via Jack Morava]
Afterword
I got onto this after lecturing on Bernstein polynomials and Bézier curves. The (constructive) proof of the Stone-Weierstrass approximation theorem in that case requires some finesse with binomial coefficients. To lighten the mood I made an off-the-cuff remark about Moriarty’s young interest in binomial coefficients, and the idea that a genuine rival for Holmes could have no background but mathematics. After lecture I started digging through some references and was led to Newcomb.
I later pointed out that, although Holmes scoffs when in their first meeting Dr Watson makes the comparison, Holmes was himself modeled on C. Auguste Dupin, who first appeared in “The Murders in the Rue Morgue” (1841) by Edgar Allan Poe (†1849 in Baltimore). [And Watson himself, ironically, on Poe’s anonymous narrator.]
Having begun the course with an analysis of the word “analysis”:
From the Greek ana·lysis=“up”·“to loosen”=“to loosen up”. To be compared with “dissolve”→“solve”. But not to be confused with anal·ysis—“anal” coming from “anus”, the Latin for “ring”. Which is relevant since it leads to the mathematical word “annulus”. And which illustrates that etymology is nonassociative: (ana)·(lysis)≠(anal)·(ysis). Don’t you think it’s a little strange, though, that the Greek and Latin are not entirely unrelated?
I ended with the opening of “Rue Morgue”:
The mental features discoursed of as the analytical, are, in themselves, but little susceptible of analysis. We appreciate them only in their effects. We know of them, among other things, that they are always to their possessor, when inordinately possessed, a source of the liveliest enjoyment. As the strong man exults in his physical ability, delighting in such exercises as call his muscles into action, so glories the analyst in that moral activity which disentangles. He derives pleasure from even the most trivial occupations bringing his talent into play. He is fond of enigmas, of conundrums, of hieroglyphics; exhibiting in his solutions of each a degree of acumen which appears to the ordinary apprehension præternatural. His results, brought about by the very soul and essence of method, have, in truth, the whole air of intuition.
The faculty of re-solution is possibly much invigorated by mathematical study, and especially by that highest branch of it which, unjustly, and merely on account of its retrograde operations, has been called, as if par excellence, analysis. Yet to calculate is not in itself to analyse. A chess-player, for example, does the one without effort at the other. It follows that the game of chess, in its effects upon mental character, is greatly misunderstood. I am not now writing a treatise, but simply prefacing a somewhat peculiar narrative by observations very much at random…
[As an aside, I visited Thomas Browne’s monument in Norwich this summer. His Hydriotaphia, Urn Burial, or, a Discourse of the Sepulchral Urns lately found in Norfolk (1658)—from which Poe’s epigraph is taken—is otherworldly.]
Observe that the opening paragraph of Poe’s manuscript did not survive to the printed edition:
“It is not improbable that a few further steps in phrenological science will lead to a belief in the existence, if not to the actual discovery and location of an organ of analysis.”
 [Moriarty, incidentally, had an associate named McTague in the 1899 play Sherlock Holmes, cowritten by Doyle and William Gillette. In fact, “Lightfoot” McTague appears in the 1916 silent film adaptation of the play, considered among the holy grails of lost films until a nitrate dupe negative was discovered mislabeled in the vaults of the Cinémathèque Française in 2014. For a far more cinematic appearance of a McTague in silent film, however, see Erich von Stroheim’s 1924 masterpiece film adaptation Greed of Frank Norris’s 1899 novel McTeague. [Is it a coincidence that McTeague and the Holmes play both date to 1899?] Seeing Greed at Eastman House inspired me to recreate one of its famous title cards—compare with the original and notice that the recreation even shakes like a projected film (the CSS for this relies on Bézier curves).]
[Moriarty, incidentally, had an associate named McTague in the 1899 play Sherlock Holmes, cowritten by Doyle and William Gillette. In fact, “Lightfoot” McTague appears in the 1916 silent film adaptation of the play, considered among the holy grails of lost films until a nitrate dupe negative was discovered mislabeled in the vaults of the Cinémathèque Française in 2014. For a far more cinematic appearance of a McTague in silent film, however, see Erich von Stroheim’s 1924 masterpiece film adaptation Greed of Frank Norris’s 1899 novel McTeague. [Is it a coincidence that McTeague and the Holmes play both date to 1899?] Seeing Greed at Eastman House inspired me to recreate one of its famous title cards—compare with the original and notice that the recreation even shakes like a projected film (the CSS for this relies on Bézier curves).]
Comments on a Paper of Karcher
Some comments on Hermann Karcher’s beautiful paper:
H. Karcher, Submersions via Projections, Geom. Dedicata 74 (1999), no. 3, pp. 249–260, MR1669359.
- Formulas (10), (11), (12) may be written: $$\begin{align*} R(X,Y)V &= -\overbrace{R(X,Y)\mathcal{H}\cdot V}^{\text{in $HM$}} + \overbrace{R^{\mathrm{V}}(X,Y)V-\big[\nabla_X\mathcal{H},\nabla_Y\mathcal{H}\big]V}^{\text{in $VM$}} \\ R(X,Y)H &= \phantom{-}\underbrace{R(X,Y)\mathcal{H}\cdot H}_{\text{in $VM$}} + \underbrace{R^{\mathrm{H}}(X,Y)H-\big[\nabla_X\mathcal{H},\nabla_Y\mathcal{H}\big] H}_{\text{in $HM$}} \end{align*}$$
- The last formula of (15) may be written: $$ (\nabla_Xg_\epsilon)(Y,Z) = \epsilon(\epsilon-2)\cdot g(Y,\nabla_X\mathcal{V}\cdot Z) $$
- The equations (16) for the difference tensor $\Gamma^\epsilon(X,Y)=\nabla_XY-\nabla^\epsilon_XY$ extend to a single general formula: $$ \Gamma^\epsilon(X,Y) = \epsilon(2-\epsilon)\cdot\big(\nabla_{\mathcal{H}X}\mathcal{H}\cdot\mathcal{V}Y +\nabla_{\mathcal{H}Y}\mathcal{H}\cdot\mathcal{V}X +\nabla_{\mathcal{V}X}\mathcal{H}\cdot\mathcal{V}Y\big) $$ The first and third terms combine easily but $\Gamma^\epsilon$—being the difference of torsion free connections—is symmetric, and this three-term formula showcases that symmetry—the third term being symmetric according to (63). Some useful special cases: $$\begin{align*} \Gamma^\epsilon(X,V) &= \epsilon(2-\epsilon)\cdot\nabla_X\mathcal{H}\cdot V \\ \Gamma^\epsilon(X,H) &= \epsilon(2-\epsilon)\cdot\nabla_H\mathcal{H}\cdot\mathcal{V}X \end{align*}$$ Comparing with (9) leads to: $$\begin{align*} (\nabla^2\pi)(X,Y) &= D\pi\cdot\Gamma^1(X,Y) \end{align*}$$
- Some formulas worth recording: $$\begin{align*} \nabla_X^\epsilon\mathcal{H}\cdot H &= \nabla_X\mathcal{H}\cdot H \\ \nabla_X^\epsilon\mathcal{H}\cdot V &= (1-\epsilon)^2\cdot\nabla_X\mathcal{H}\cdot V \\ \big[\nabla^\epsilon_X\mathcal{H},\nabla^\epsilon_Y\mathcal{H}\big] &= (1-\epsilon)^2\cdot \big[\nabla_X\mathcal{H},\nabla_Y\mathcal{H}\big] \end{align*}$$ Note that the second equation says that the second fundamental forms of the fibers go to zero as $\epsilon\to1$.
For this and more, see my paper:
C. McTague, Shrinking the Fibers of a Submersion Splits the Riemann Tensor (2015).
Computing Hirzebruch L-Polynomials
Andrew Ranicki recently asked me to compute the Hirzebruch L-polynomial L8 expressing the signature of a 32-dimensional manifold in terms of its Pontrjagin numbers. (Hirzebruch’s book Topological Methods in Algebraic Geometry only lists L1 through L5, in §1.5.)
Here is Mathematica code to compute it, or any other member of a multiplicative sequence of polynomials:
K[Q_,n_Integer] := Module[{z,x},
SymmetricReduction[
SeriesCoefficient[
Product[ComposeSeries[Series[Q[z],{z,0,n}],
Series[x[i]z,{z,0,n}]],{i,1,n}],n],
Table[x[i],{i,1,n}],
Table[Subscript[c,i],{i,1,n}]][[1]] // FactorTerms]
The generating series for the L-sequence is $\frac{\sqrt{z}}{\tanh\sqrt{z}}$ so L8 can then be computed by running:
K[ Sqrt[#]/Tanh[Sqrt[#]]&, 8] /. c->p
which produces:
$\hspace{-30pt}L_8=\frac{1}{488462349375}\left(355554717 p_8-63136017 p_1 p_7-18909191 p_2 p_6+15043799 p_1^2 p_6-5468617 p_3 p_5+8640058 p_1 p_2 p_5-3750699 p_1^3 p_5-1334163 p_4^2+2843653 p_1 p_3 p_4+1311182 p_2^2 p_4-3307215 p_1^2 p_2 p_4+972066 p_1^4 p_4+679224 p_2 p_3^2-825291 p_1^2 p_3^2-1250470 p_1 p_2^2 p_3+1371584 p_1^3 p_2 p_3-286966 p_1^5 p_3-68435 p_2^4+423040 p_1^2 p_2^3-407726 p_1^4 p_2^2+122508 p_1^6 p_2-10851 p_1^8\right)$
Some other L-polynomials (now published as OEIS sequence A237111):
$\hspace{-30pt}L_1=\frac{1}{3}p_1$
$\hspace{-30pt}L_2=\frac{1}{45}\left(7 p_2-p_1^2\right)$
$\hspace{-30pt}L_3=\frac{1}{945}\left(62 p_3-13 p_1 p_2+2 p_1^3\right)$
$\hspace{-30pt}L_4=\frac{1}{14175}\left(381 p_4-71 p_1 p_3-19 p_2^2+22 p_1^2 p_2-3 p_1^4\right)$
$\hspace{-30pt}L_5=\frac{1}{467775}\left(5110 p_5-919 p_1 p_4-336 p_2 p_3+237 p_1^2 p_3+127 p_1 p_2^2-83 p_1^3 p_2+10 p_1^5\right)$
$\hspace{-30pt}L_6=\frac{1}{638512875}\left(2828954 p_6-503904 p_1 p_5-159287 p_2 p_4+122523 p_1^2 p_4-40247 p_3^2+86901 p_1 p_2 p_3-33863 p_1^3 p_3+8718 p_2^3-27635 p_1^2 p_2^2+12842 p_1^4 p_2-1382 p_1^6\right)$
$\hspace{-30pt}L_7=\frac{1}{1915538625}\left(3440220 p_7-611266 p_1 p_6-185150 p_2 p_5+146256 p_1^2 p_5-62274 p_3 p_4+88137 p_1 p_2 p_4-37290 p_1^3 p_4+22027 p_1 p_3^2+16696 p_2^2 p_3-39341 p_1^2 p_2 p_3+10692 p_1^4 p_3-7978 p_1 p_2^3+11880 p_1^3 p_2^2-4322 p_1^5 p_2+420 p_1^7\right)$
$\hspace{-30pt}L_8=\frac{1}{488462349375}\left(355554717 p_8-63136017 p_1 p_7-18909191 p_2 p_6+15043799 p_1^2 p_6-5468617 p_3 p_5+8640058 p_1 p_2 p_5-3750699 p_1^3 p_5-1334163 p_4^2+2843653 p_1 p_3 p_4+1311182 p_2^2 p_4-3307215 p_1^2 p_2 p_4+972066 p_1^4 p_4+679224 p_2 p_3^2-825291 p_1^2 p_3^2-1250470 p_1 p_2^2 p_3+1371584 p_1^3 p_2 p_3-286966 p_1^5 p_3-68435 p_2^4+423040 p_1^2 p_2^3-407726 p_1^4 p_2^2+122508 p_1^6 p_2-10851 p_1^8\right)$
$\hspace{-30pt}L_9=\frac{1}{194896477400625}\left(57496915570 p_9-10208138209 p_1 p_8-3048553630 p_2 p_7+2429800789 p_1^2 p_7-844282766 p_3 p_6+1377913993 p_1 p_2 p_6-602296505 p_1^3 p_6-271389940 p_4 p_5+388346645 p_1 p_3 p_5+194787260 p_2^2 p_5-503353722 p_1^2 p_2 p_5+151701815 p_1^4 p_5+93946261 p_1 p_4^2+130062108 p_2 p_3 p_4-164047713 p_1^2 p_3 p_4-150462162 p_1 p_2^2 p_4+176155388 p_1^3 p_2 p_4-39714485 p_1^5 p_4+12765448 p_3^3-78021660 p_1 p_2 p_3^2+44101890 p_1^3 p_3^2-20200592 p_2^3 p_3+100397374 p_1^2 p_2^2 p_3-70683311 p_1^4 p_2 p_3+12038553 p_1^6 p_3+11098737 p_1 p_2^4-29509334 p_1^3 p_2^3+20996751 p_1^5 p_2^2-5391213 p_1^7 p_2+438670 p_1^9\right)$
$\hspace{-30pt}L_{10}=\frac{1}{32157918771103125}\left(3844943648994 p_{10}-682613292644 p_1 p_9-203707792197 p_2 p_8+162436741673 p_1^2 p_8-55782134394 p_3 p_7+91819476941 p_1 p_2 p_7-40205725073 p_1^3 p_7-15408421872 p_4 p_6+24755004136 p_1 p_3 p_6+12733594519 p_2^2 p_6-33128200250 p_1^2 p_2 p_6+10051904387 p_1^4 p_6-3689436247 p_5^2+7860847666 p_1 p_4 p_5+7156900191 p_2 p_3 p_5-9206843259 p_1^2 p_3 p_5-9177195410 p_1 p_2^2 p_5+11001659873 p_1^3 p_2 p_5-2541992887 p_1^5 p_5+1745258589 p_2 p_4^2-2219530950 p_1^2 p_4^2+1300052223 p_3^2 p_4-6094105875 p_1 p_2 p_3 p_4+3572462273 p_1^3 p_3 p_4-932098945 p_2^3 p_4+4896089605 p_1^2 p_2^2 p_4-3669438754 p_1^4 p_2 p_4+671189161 p_1^6 p_4-597952583 p_1 p_3^3-750509715 p_2^2 p_3^2+2548895877 p_1^2 p_2 p_3^2-923938550 p_1^4 p_3^2+1322085815 p_1 p_2^3 p_3-2812761078 p_1^3 p_2^2 p_3+1451051181 p_1^5 p_2 p_3-208588561 p_1^7 p_3+46251222 p_2^5-471455695 p_1^2 p_2^4+768892622 p_1^4 p_2^3-433817957 p_1^6 p_2^2+97463470 p_1^8 p_2-7333662 p_1^{10}\right)$
$\hspace{-30pt}L_{11}=\frac{1}{2218896395206115625}\left(107522567547780 p_{11}-19088863620918 p_1 p_{10}-5695530073310 p_2 p_9+4542143981708 p_1^2 p_9-1555173021402 p_3 p_8+2565423874181 p_1 p_2 p_8-1123840932470 p_1^3 p_8-411527701200 p_4 p_7+683711631540 p_1 p_3 p_7+354034647890 p_2^2 p_7-922678415929 p_1^2 p_2 p_7+280446917930 p_1^4 p_7-129278298520 p_5 p_6+186412296664 p_1 p_4 p_6+189226541336 p_2 p_3 p_6-244992687206 p_1^2 p_3 p_6-250388515289 p_1 p_2^2 p_6+302166509321 p_1^3 p_2 p_6-70283925270 p_1^5 p_6+44421264839 p_1 p_5^2+60174415980 p_2 p_4 p_5-77314873002 p_1^2 p_4 p_5+27308760472 p_3^2 p_5-139409773867 p_1 p_2 p_3 p_5+83319979706 p_1^3 p_3 p_5-23080275470 p_2^3 p_5+123981810568 p_1^2 p_2^2 p_5-95102983271 p_1^4 p_2 p_5+17820178690 p_1^6 p_5+13901765658 p_3 p_4^2-33935234091 p_1 p_2 p_4^2+20066965081 p_1^3 p_4^2-25211090659 p_1 p_3^2 p_4-23432247682 p_2^2 p_3 p_4+82201241803 p_1^2 p_2 p_3 p_4-30872129848 p_1^4 p_3 p_4+25074247417 p_1 p_2^3 p_4-56265244569 p_1^3 p_2^2 p_4+30821702183 p_1^5 p_2 p_4-4743504310 p_1^7 p_4-4701152064 p_2 p_3^3+8079666657 p_1^2 p_3^3+20273980429 p_1 p_2^2 p_3^2-29454532487 p_1^3 p_2 p_3^2+7815215137 p_1^5 p_3^2+2684318680 p_2^4 p_3-22975754625 p_1^2 p_2^3 p_3+29852017156 p_1^4 p_2^2 p_3-12130331601 p_1^6 p_2 p_3+1509537376 p_1^8 p_3-1620540574 p_1 p_2^5+6744992170 p_1^3 p_2^4-7829491106 p_1^5 p_2^3+3662998844 p_1^7 p_2^2-732652806 p_1^9 p_2+51270780 p_1^{11}\right)$
$\hspace{-30pt}L_{12}=\frac{1}{3028793579456347828125}\left(59482964049337110 p_{12}-10560195815097210 p_1 p_{11}-3150694647926016 p_2 p_{10}+2512728757752768 p_1^2 p_{10}-859683903320810 p_3 p_9+1418912367890776 p_1 p_2 p_9-621655204655468 p_1^3 p_9-224971539271761 p_4 p_8+377051717854661 p_1 p_3 p_8+195571661859765 p_2^2 p_8-509919773356306 p_1^2 p_2 p_8+155056838434481 p_1^4 p_8-60744246118110 p_5 p_7+98470681343871 p_1 p_4 p_7+103164098432426 p_2 p_3 p_7-133798852640129 p_1^2 p_3 p_7-137649995502241 p_1 p_2^2 p_7+166399979251074 p_1^3 p_2 p_7-38770694005481 p_1^5 p_7-14410087794673 p_6^2+30742795880856 p_1 p_5 p_6+28042926014435 p_2 p_4 p_6-36219404128521 p_1^2 p_4 p_6+13840906762108 p_3^2 p_6-72790761663197 p_1 p_2 p_3 p_6+43779115251039 p_1^3 p_3 p_6-12351564858777 p_2^3 p_6+66784338642637 p_1^2 p_2^2 p_6-51565502511583 p_1^4 p_2 p_6+9726168419869 p_1^6 p_6+6690315663313 p_2 p_5^2-8610718021212 p_1^2 p_5^2+9009316465271 p_3 p_4 p_5-23053514535432 p_1 p_2 p_4 p_5+13772029163489 p_1^3 p_4 p_5-10424737212619 p_1 p_3^2 p_5-10349150762991 p_2^2 p_3 p_5+36980302520182 p_1^2 p_2 p_3 p_5-14155214042120 p_1^4 p_3 p_5+12199190282918 p_1 p_2^3 p_5-27983496067711 p_1^3 p_2^2 p_5+15683170260164 p_1^5 p_2 p_5-2471593910869 p_1^7 p_5+871756041250 p_4^3-5299281214631 p_1 p_3 p_4^2-2544205275373 p_2^2 p_4^2+9000337394702 p_1^2 p_2 p_4^2-3410474361584 p_1^4 p_4^2-3803158108206 p_2 p_3^2 p_4+6677705750121 p_1^2 p_3^2 p_4+12382204834839 p_1 p_2^2 p_3 p_4-18566411153047 p_1^3 p_2 p_3 p_4+5099150967499 p_1^5 p_3 p_4+945948441582 p_2^4 p_4-8478203154675 p_1^2 p_2^3 p_4+11595957601472 p_1^4 p_2^2 p_4-4991726989557 p_1^6 p_2 p_4+663128304922 p_1^8 p_4-206345908947 p_3^4+2489517554874 p_1 p_2 p_3^3-1830324992020 p_1^3 p_3^3+1052197012244 p_2^3 p_3^2-6891343720499 p_1^2 p_2^2 p_3^2+6109565322130 p_1^4 p_2 p_3^2-1275465567049 p_1^6 p_3^2-1828977466670 p_1 p_2^4 p_3+6374277369326 p_1^3 p_2^3 p_3-5871050509546 p_1^5 p_2^2 p_3+1966494037756 p_1^7 p_2 p_3-215864759622 p_1^9 p_3-44720298010 p_2^6+679976646780 p_1^2 p_2^5-1676297291469 p_1^4 p_2^4+1502303537032 p_1^6 p_2^3-600842521854 p_1^8 p_2^2+108419277660 p_1^{10} p_2-7090922730 p_1^{12}\right)$
$\hspace{-30pt}L_{13}=\frac{1}{9086380738369043484375}\left(72322615121247036 p_{13}-12839651071909926 p_1 p_{12}-3830739593311176 p_2 p_{11}+3055097425061946 p_1^2 p_{11}-1045049756196264 p_3 p_{10}+1725094701581424 p_1 p_2 p_{10}-755821122963534 p_1^3 p_{10}-272712748239906 p_4 p_9+458078601115360 p_1 p_3 p_9+237699842426306 p_2^2 p_9-619830309829310 p_1^2 p_2 p_9+188499057034344 p_1^4 p_9-70565079148746 p_5 p_8+118306288116891 p_1 p_4 p_8+124969620711936 p_2 p_3 p_8-162151396044763 p_1^2 p_3 p_8-167097801278477 p_1 p_2^2 p_8+202085845024907 p_1^3 p_2 p_8-47105612724954 p_1^5 p_8-21922060368516 p_6 p_7+31742893399152 p_1 p_5 p_7+32491662944022 p_2 p_4 p_7-42035081558097 p_1^2 p_4 p_7+16441304584404 p_3^2 p_7-87179794392340 p_1 p_2 p_3 p_7+52522473118357 p_1^3 p_3 p_7-14890478221466 p_2^3 p_7+80649517416487 p_1^2 p_2^2 p_7-62376843431291 p_1^4 p_2 p_7+11785293691794 p_1^6 p_7+7511972573843 p_1 p_6^2+10136863360022 p_2 p_5 p_6-13080453013002 p_1^2 p_5 p_6+8993483945286 p_3 p_4 p_6-23579084234895 p_1 p_2 p_4 p_6+14158404892491 p_1^3 p_4 p_6-11593881767582 p_1 p_3^2 p_6-11781330593106 p_2^2 p_3 p_6+42359270842707 p_1^2 p_2 p_3 p_6-16315258400629 p_1^4 p_3 p_6+14320243955795 p_1 p_2^3 p_6-33061727161314 p_1^3 p_2^2 p_6+18650010728593 p_1^5 p_2 p_6-2958448000074 p_1^7 p_6+2170310001860 p_3 p_5^2-5616857698569 p_1 p_2 p_5^2+3362197563453 p_1^3 p_5^2+1598325532596 p_4^2 p_5-7521438548927 p_1 p_3 p_4 p_5-3747037194988 p_2^2 p_4 p_5+13387399017752 p_1^2 p_2 p_4 p_5-5124542468415 p_1^4 p_4 p_5-3386244167460 p_2 p_3^2 p_5+6038413635675 p_1^2 p_3^2 p_5+11951705360023 p_1 p_2^2 p_3 p_5-18248868443891 p_1^3 p_2 p_3 p_5+5106691054163 p_1^5 p_3 p_5+983844985516 p_2^4 p_5-9004069487482 p_1^2 p_2^3 p_5+12584826999985 p_1^4 p_2^2 p_5-5540530920427 p_1^6 p_2 p_5+753423126204 p_1^8 p_5-726569491346 p_1 p_4^3-1736384753736 p_2 p_3 p_4^2+3069125281035 p_1^2 p_3 p_4^2+2939216673351 p_1 p_2^2 p_4^2-4444873416929 p_1^3 p_2 p_4^2+1231788304752 p_1^5 p_4^2-444806806572 p_3^3 p_4+4390275986442 p_1 p_2 p_3^2 p_4-3296411478022 p_1^3 p_3^2 p_4+1358265174044 p_2^3 p_3 p_4-9151640683451 p_1^2 p_2^2 p_3 p_4+8367077111912 p_1^4 p_2 p_3 p_4-1806365634680 p_1^6 p_3 p_4-1396161717978 p_1 p_2^4 p_4+5087384629390 p_1^3 p_2^3 p_4-4923620079719 p_1^5 p_2^2 p_4+1743201389284 p_1^7 p_2 p_4-203721801174 p_1^9 p_4+238460897625 p_1 p_3^4+418208554632 p_2^2 p_3^3-1845509565666 p_1^2 p_2 p_3^3+827899012917 p_1^4 p_3^3-1560693825696 p_1 p_2^3 p_3^2+4159635712346 p_1^3 p_2^2 p_3^2-2612096050645 p_1^5 p_2 p_3^2+448999445468 p_1^7 p_3^2-126439832080 p_2^5 p_3+1660385531550 p_1^2 p_2^4 p_3-3418480202739 p_1^4 p_2^3 p_3+2422033713280 p_1^6 p_2^2 p_3-689846708628 p_1^8 p_2 p_3+67770375018 p_1^{10} p_3+81719534070 p_1 p_2^6-490242029730 p_1^3 p_2^5+838678611984 p_1^5 p_2^4-610634946312 p_1^7 p_2^3+213434336190 p_1^9 p_2^2-35110888158 p_1^{11} p_2+2155381956 p_1^{13}\right)$
$\hspace{-30pt}L_{14}=\frac{1}{3952575621190533915703125}\left(12750394707149844332 p_{14}-2263615514569024112 p_1 p_{13}-675353005134411002 p_2 p_{12}+538609557138247922 p_1^2 p_{12}-184232237840795732 p_3 p_{11}+304128001945086214 p_1 p_2 p_{11}-133249477483117322 p_1^3 p_{11}-48042776207167238 p_4 p_{10}+80742799399504690 p_1 p_3 p_{10}+41902383906298496 p_2^2 p_{10}-109268418713940708 p_1^2 p_2 p_{10}+33230958341836400 p_1^4 p_{10}-12295169263985832 p_5 p_9+20794596976366700 p_1 p_4 p_9+22011574730657134 p_2 p_3 p_9-28563786972400662 p_1^2 p_3 p_9-29447481485141260 p_1 p_2^2 p_9+35617257910457980 p_1^3 p_2 p_9-8303170596462900 p_1^5 p_9-3283777774068218 p_6 p_8+5347010561485880 p_1 p_5 p_8+5657331509067973 p_2 p_4 p_8-7322263634985679 p_1^2 p_4 p_8+2881472301806105 p_3^2 p_8-15311255840106597 p_1 p_2 p_3 p_8+9228451340334101 p_1^3 p_3 p_8-2619556019278058 p_2^3 p_8+14194112098851433 p_1^2 p_2^2 p_8-10982871479970858 p_1^4 p_2 p_8+2075954705219238 p_1^6 p_8-775554762561166 p_7^2+1656188545755730 p_1 p_6 p_7+1515196827131834 p_2 p_5 p_7-1957838195748202 p_1^2 p_5 p_7+1498643293045570 p_3 p_4 p_7-3959880502362187 p_1 p_2 p_4 p_7+2381631835724001 p_1^3 p_4 p_7-1996126430113095 p_1 p_3^2 p_7-2041551434526030 p_2^2 p_3 p_7+7352710942428867 p_1^2 p_2 p_3 p_7-2836758879081301 p_1^4 p_3 p_7+2501988111691518 p_1 p_2^3 p_7-5786202450321413 p_1^3 p_2^2 p_7+3269478592431558 p_1^5 p_2 p_7-519509387477238 p_1^7 p_7+358529951749599 p_2 p_6^2-462741237149047 p_1^2 p_6^2+470192290021650 p_3 p_5 p_6-1232603833449492 p_1 p_2 p_5 p_6+739752938870166 p_1^3 p_5 p_6+211252827690392 p_4^2 p_6-1087286066381534 p_1 p_3 p_4 p_6-552091543508825 p_2^2 p_4 p_6+1982493137575544 p_1^2 p_2 p_4 p_6-762727300689629 p_1^4 p_4 p_6-541960519119831 p_2 p_3^2 p_6+972130079657535 p_1^2 p_3^2 p_6+1969271080274147 p_1 p_2^2 p_3 p_6-3025304042558420 p_1^3 p_2 p_3 p_6+851815550847629 p_1^5 p_3 p_6+166069974113788 p_2^4 p_6-1529551857415271 p_1^2 p_2^3 p_6+2151552906683779 p_1^4 p_2^2 p_6-953358066833460 p_1^6 p_2 p_6+130486561787496 p_1^8 p_6+106559517148035 p_4 p_5^2-262056856899985 p_1 p_3 p_5^2-131811132313665 p_2^2 p_5^2+471919294342151 p_1^2 p_2 p_5^2-181038396627908 p_1^4 p_5^2-192614659760042 p_1 p_4^2 p_5-353063374913277 p_2 p_3 p_4 p_5+629541942510225 p_1^2 p_3 p_4 p_5+625456789776172 p_1 p_2^2 p_4 p_5-955204796916125 p_1^3 p_2 p_4 p_5+267390046588279 p_1^5 p_4 p_5-53363251821705 p_3^3 p_5+564108245216523 p_1 p_2 p_3^2 p_5-430070096737136 p_1^3 p_3^2 p_5+185786489726488 p_2^3 p_3 p_5-1273653276229747 p_1^2 p_2^2 p_3 p_5+1185467415261029 p_1^4 p_2 p_3 p_5-260700468307217 p_1^6 p_3 p_5-209198940940456 p_1 p_2^4 p_5+778136940573984 p_1^3 p_2^3 p_5-769326245733787 p_1^5 p_2^2 p_5+278476291878048 p_1^7 p_2 p_5-33301833373996 p_1^9 p_5-34286351316642 p_2 p_4^3+60774217415757 p_1^2 p_4^3-42598384142751 p_3^2 p_4^2+289343407856985 p_1 p_2 p_3 p_4^2-218728278954802 p_1^3 p_3 p_4^2+46158975519344 p_2^3 p_4^2-313545353277647 p_1^2 p_2^2 p_4^2+289129284242879 p_1^4 p_2 p_4^2-62985004440353 p_1^6 p_4^2+74063033154267 p_1 p_3^3 p_4+104089783176396 p_2^2 p_3^2 p_4-468286854355998 p_1^2 p_2 p_3^2 p_4+214458461172387 p_1^4 p_3^2 p_4-289335556881588 p_1 p_2^3 p_3 p_4+792778821013802 p_1^3 p_2^2 p_3 p_4-512994873378385 p_1^5 p_2 p_3 p_4+91106047648244 p_1^7 p_3 p_4-13272078302266 p_2^5 p_4+181225720113282 p_1^2 p_2^4 p_4-389536967694841 p_1^4 p_2^3 p_4+289501185106240 p_1^6 p_2^2 p_4-86977563536574 p_1^8 p_2 p_4+9073973574034 p_1^{10} p_4+11475032305464 p_2 p_3^4-25480617652053 p_1^2 p_3^4-89349671976612 p_1 p_2^2 p_3^3+160436593965288 p_1^3 p_2 p_3^3-50969939652942 p_1^5 p_3^3-19070069854338 p_2^4 p_3^2+203682123751428 p_1^2 p_2^3 p_3^2-320496948968445 p_1^4 p_2^2 p_3^2+154690777155096 p_1^6 p_2 p_3^2-22586488151310 p_1^8 p_3^2+33078442359342 p_1 p_2^5 p_3-171075425779366 p_1^3 p_2^4 p_3+243830587870408 p_1^5 p_2^3 p_3-139882802086008 p_1^7 p_2^2 p_3+34654263473350 p_1^9 p_2 p_3-3081957515434 p_1^{11} p_3+599122543748 p_2^7-12711483862714 p_1^2 p_2^6+44064808661200 p_1^4 p_2^5-57091038739788 p_1^6 p_2^4+34963111228740 p_1^8 p_2^3-10859561841202 p_1^{10} p_2^2+1642500201244 p_1^{12} p_2-94997844116 p_1^{14}\right)$
Dürer’s Melencolia i
I recently gave a short talk about Dürer’s engraving Melencolia I (1514) in Rochelle Tobias’s seminar in the German dept at Hopkins.
To begin I talked a little about the magic square of numbers. First of all it’s “normal”: each number 1,…,16 appears once. And not only do the rows, columns and two diagonals sum to 34, so do the 4 corners, the 4 numbers in the center, and the remaining parallel segments. The bottom row serves as Dürer’s second signature: the middle two numbers form the year the engraving was made and the outer numbers correspond to Dürer’s initials A=1, D=4. It’s believed that the sum 34 refers to Dürer’s age when he engraved it, 43, reinforced by the square’s placement beside the hourglass. There was a popular magical/astrological association at the time between magic squares and planets. Saturn corresponded to 3×3 magic squares and Jupiter to 4×4. Rochelle pointed out that it makes sense for Dürer to have used a 4×4 rather than a 3×3 (Saturn is closely associated with melancholy) since things associated with Jupiter were supposed to help fend off melancholy.
The Solid
The solid in the engraving is rather mysterious and was the main subject of my talk. People have been debating it for at least the last 100 years with a possible breakthrough in 2004. The most influential work on the engraving—Raymond Klibansky’s magnum opus Saturn and Melancholy (1964)—has the least to say about the solid of all the objects in the engraving.
The solid is completely unique to the engraving and doesn’t appear anywhere else in art or mathematics. At first it was thought to simply be a cube with two edges “truncated”, that is chopped off, leaving behind triangular faces. It doesn’t quite look like a cube but it was thought that Dürer simply made a mistake with perspective. Eventually it was agreed that Dürer wasn’t the sort to make mistakes with perspective and hence that the underlying shape must not be a cube. There have been quite a few papers over the years correcting for perspective in various ways to compute what the angles of the solid are, reaching different conclusions.
The papers which most interested me were recent ones inspired by a paper of JV Field at Birkbeck:
Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler, Archive for History of Exact Sciences, Vol. 50, No. 3/4 (September 1997), pp. 241-289.
I probably found that paper the most interesting of the lot. It’s on the history of Archimedean solids. The simplest solids of all are the Platonic solids, solids like the cube whose faces are all the same shape and size.
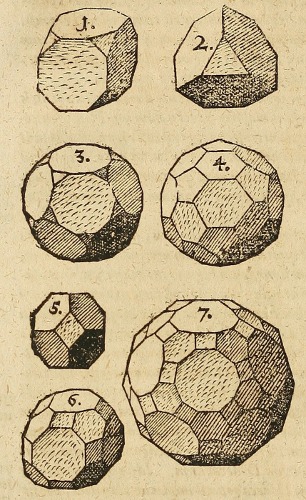
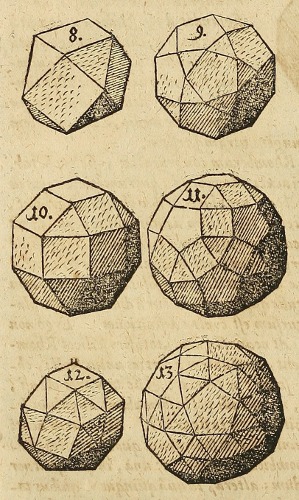 The ancient Greeks showed that there are just 5 of them—the tetrahedron, the hexahedron (=cube), the octahedron, the dodecahedron, and the icosahedron—and they used them as the basis for theories about the physical universe. The next simplest solids are the Archimedean solids, solids whose vertices are all “the same” but whose faces are not. The ancient Greeks determined that there are just 13 of them (or 15 depending on how you count—2 of the 13 differ from their mirror images). One of the last great ancient Greek mathematicians Pappus listed all 13 of them, credited their discovery to Archimedes, but instead of drawing them cryptically wrote the total number of triangles, squares, pentagons,… each had. His work was correct but apparently forgotten—for more than a thousand years—until in 1619 Johannes Kepler published a complete list including drawings of each (reproduced above).
The ancient Greeks showed that there are just 5 of them—the tetrahedron, the hexahedron (=cube), the octahedron, the dodecahedron, and the icosahedron—and they used them as the basis for theories about the physical universe. The next simplest solids are the Archimedean solids, solids whose vertices are all “the same” but whose faces are not. The ancient Greeks determined that there are just 13 of them (or 15 depending on how you count—2 of the 13 differ from their mirror images). One of the last great ancient Greek mathematicians Pappus listed all 13 of them, credited their discovery to Archimedes, but instead of drawing them cryptically wrote the total number of triangles, squares, pentagons,… each had. His work was correct but apparently forgotten—for more than a thousand years—until in 1619 Johannes Kepler published a complete list including drawings of each (reproduced above).
In the meantime though quite a few Renaissance artists unaware of Pappus’s work had had a go at constructing them, among them Dürer. There’s a great table in Field’s paper listing which of the solids each of four artists is known to have constructed:
| JK no | Name | Piero | Pacioli | Dürer | Barbaro |
|---|---|---|---|---|---|
| 1 | truncated cube | L | — | √ | √ |
| 2 | tr. tetrahedron | T,L | √ | √ | √ |
| 3 | tr. dodecahedron | L | — | — | √ |
| 4 | tr. icosahedron | L | √ | — | √ |
| 5 | tr. octahedron | L | √ | √ | √ |
| 6 | tr. cuboctahedron | — | — | √ | √ |
| 7 | tr. icosidodecahedron | — | — | — | √ |
| 8 | cuboctahedron | T | √ | √ | √ |
| 9 | icosidodecahedron | — | √ | — | √ |
| 10 | rhombicuboctahedron | — | √ | √ | √ |
| 11 | rhombicosidodecahedron | — | — | — | √ |
| 12 | snub cube | — | — | √ | — |
| 13 | snub dodecahedron | — | — | — | — |
The table suggests that Dürer discovered two Archimedean solids previously unknown to Renaissance artists, the truncated cuboctahedron (6) and the snub cube (12). Dürer worked in two different ways: By drawing projections onto the three coordinate planes and by making what he called a Netz—lines on paper you can cut and fold along to make a model of a solid. Dürer appears to have invented this method actually, and he used it to discover new solids.
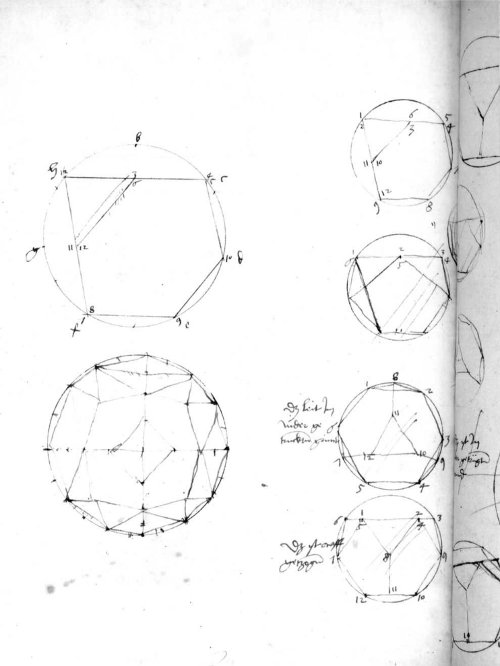 Field thinks Dürer may have been aware of all 13 solids since one can construct a Netz for each of the missing solids by small modifications to the new Netze Dürer discovered, but that Dürer didn’t write them all down because Dürer didn’t realize there are only 13 of them. Field speculates that Kepler may have learned all this from Dürer and synthesized it with the work of Pappus.
Field thinks Dürer may have been aware of all 13 solids since one can construct a Netz for each of the missing solids by small modifications to the new Netze Dürer discovered, but that Dürer didn’t write them all down because Dürer didn’t realize there are only 13 of them. Field speculates that Kepler may have learned all this from Dürer and synthesized it with the work of Pappus.
To cut to the chase, this chap Hans Weitzel found a sketch by Dürer in a library in Nürnberg in 2003 where Dürer had constructed two known Archimedean solids but on the same page had made an enigmatic drawing of a pentagon inscribed in a circle:
A further hypothesis on the polyhedron of A. Dürer’s engraving Melencolia I, Historia Mathematica, Vol. 31, Issue 1, Feb 2004, pp. 11–14.
Weitzel argues that Dürer was on that page trying to construct a new Archimedean solid which doesn’t exist (one where each vertex touches one triangle and two pentagons) and that the pentagon Dürer in the process drew exactly matches the face of the solid in the engraving. In fact Weitzel finds that the angles of the sketched pentagon agree with the corrected angles computed by others for the mystery solid. So Weitzel argues that the solid in the engraving is the result of a failed attempt by Dürer to discover a new Archimedean solid.
This seems consistent with Erwin Panofsky’s interpretation of the engraving as a spiritual self-portrait of Dürer, exploring the relationship between creative genius and melancholy. That’s the thrust of it as I understand it anyway. It’s kind of intense. That’s not even getting into black bile, the four temperaments, and the rest of it.
Saturn and Krypton—Superman as Winged Melancholia?


A week or so after my talk it suddenly struck me that Dürer’s pentagon is quite similar to the outline of Superman’s “S” shield.
This points to remarkable parallels between Melencolia I and the Superman universe.
Compare, for example, the effect of Dürer’s solid on Winged Melancholia to the effect of the Kryptonite solid on the flying figure in the panel at the far right.
Janine’s Paper Universe
One of my favorite passages from WG Sebald’s Rings of Saturn (1995) alludes to Dürer’s engraving:
“Many a time, at the end of a working day, Janine would talk to me about Flaubert’s view of the world, in her office where there were such quantities of lecture notes, letters and other documents lying around that it was like standing amidst a flood of paper. On the desk, which was both the origin and the focal point of this amazing profusion of paper, a virtual paper landscape had come into being in the course of time, with mountains and valleys. Like a glacier when it reaches the sea, it had broken off at the edges and established new deposits all around on the floor, which in turn were advancing imperceptibly towards the centre of the room. Years ago, Janine had been obliged by the ever-increasing masses of paper on her desk to bring further tables into use, and these tables, where similar processes of accretion had subsequently taken place, represented later epochs, so to speak, in the evolution of Janine’s paper universe. The carpet, too, had long since vanished beneath several inches of paper; indeed, the paper had begun climbing from the floor, on which, year after year, it had settled, and was now up the walls as high as the top of the door frame, page upon page of memoranda and notes pinned up in multiple layers, all of them by just one corner. Wherever it was possible there were piles of papers on the books on her shelves as well. It once occurred to me that at dusk, when all of this paper seemed to gather into itself the pallor of the fading light, it was like the snow in the fields, long ago, beneath the ink-black sky. In the end Janine was reduced to working from an easychair drawn more or less into the middle of her room where, if one passed her door, which was always ajar, she could be seen bent almost double scribbling on a pad on her knees or sometimes just lost in thought. Once when I remarked that sitting there amidst her papers she resembled the angel in Dürer’s Melancholia, steadfast among the instruments of destruction, her response was that the apparent chaos surrounding her represented in reality a perfect kind of order, or an order which at least tended towards perfection. And the fact was that whatever she might be looking for amongst her papers or her books, or in her head, she was generally able to find right away.”
References
- Johannes Kepler, Harmonices Mundi libri V, Linz, 1619.
- Erwin Panofsky, The Life and Art of Albrecht Dürer, Princeton, 1955.
- Raymond Klibansky, Erwin Panofsky & Fritz Saxl. Saturn and Melancholy. Studies in the History of Natural Philosophy, Religion, and Art, London, 1964.
- Klaus-Peter Schuster, Melencolia I. Dürers Denkbild. Dissertation. Universität Göttingen 1975. Berlin 1991.
- Terence Lynch, The Geometric Body in Dürer’s Engraving Melencolia I, Journal of the Warburg and Courtauld Institutes, Vol. 45, (1982), pp. 226-232.
- JV Field. Rediscovering the Archimedean Polyhedra: Piero della Francesca, Luca Pacioli, Leonardo da Vinci, Albrecht Dürer, Daniele Barbaro, and Johannes Kepler. Archive for History of Exact Sciences, Vol. 50, No. 3/4 (September 1997), pp. 241-289.
- Peter Schreiber, A New Hypothesis on Dürer’s Enigmatic Polyhedron in His Copper Engraving “Melencolia I”, Historia Mathematica, Vol. 26, Issue 4, Nov 1999, pp. 369–377.
- Hans Weitzel, A further hypothesis on the polyhedron of A. Dürer’s engraving Melencolia I, Historia Mathematica, Vol. 31, Issue 1, Feb 2004, pp. 11–14.
- Hans Weitzel, Zum Polyeder auf A. Dürers Stich Melencolia I — ein Nürnberger Skizzenblatt mit Darstellungen archimedischer Körper, Sudhoffs Archiv, Bd. 91, H. 2 (2007), pp. 129–173.
« Previous Page — Next Page »

